今回は、数学IA「メネラウスの定理」の証明をしていきます。
メネラウスの定理って?
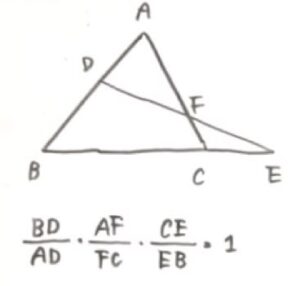
メネラウスの定理とは、ある直線(上の図のDE)が、三角形(今回で言えば三角形ABC)の頂点を通らずに2点で交わるときに
BD/AD・AF/FC・CE/EB=1
が成り立つという定理です。
動画でも解説をしています。
図形を用いた証明なので、動画での解説がおすすめです▼
メネラウスの定理の証明
BD/AD・AF/FC・CE/EB=1 …①とします。
メネラウスの定理を証明をするときに、次の考え方を使います。
考え方
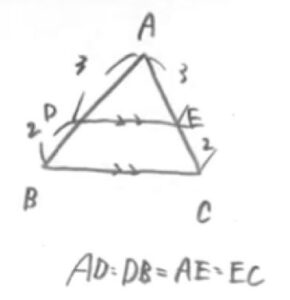
上図のように、三角形ABCの中に辺BCと平行な直線DEがあった場合、「AD:DB=AE:ECになる」という性質を使っていきます。
DEと平行な直線を1本引きます(直線HC)
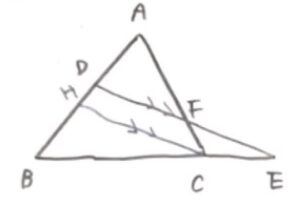
まず三角形AHCで考えると
AF:FC=AD:DHなので
AF/FC=AD/DH …②
次に三角形BDEで考えると
CE:BE=DH:BDなので
CE/BE=DH/BD …③
②、③の式を①に代入すると
BD/AD✕AD/DH✕DH/BD=1となるので
メネラウスの定理が成り立ちます。
fa-smile-o「補助線HC」と「辺の比」を利用すればメネラウスの定理の証明ができるので、覚えておきましょうね。
難しかった人は、一度解説動画で確認してみてくださいね。
StanyOnline
StanyOnlineでは
- 最短経路の合格をサポートする「受験コーチング」
- 家庭学習で行き詰まった問題をチャットで解決できる「質問し放題チャット家庭教師」
- 東大、京大、早慶などの難関大講師が授業を行う「オンライン家庭教師」
などの、様々なオンラインサービスを提供しております。
「受験コーチング」、「質問し放題のチャット家庭教師」は1週間の無料体験、
「Zoomオンライン家庭教師」は1コマ(2000円分)を無料で体験いただけます。
ぜひお気軽にお問い合わせください!
\まずは無料で体験/










