今回は、正弦定理の証明の解説をします。
【正弦定理】a/sinA=b/sinB=c/sinC=2R
動画でも解説しています。詳しい解説を見たい方は下の動画をご覧ください。
【4分で分かる】正弦定理の証明
【正弦定理】a/sinA=b/sinB=c/sinC=2R
の証明を行っていきます。
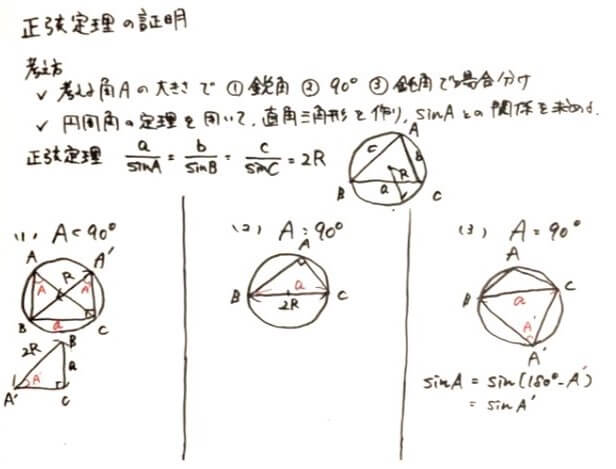
考え方
- 考える角Aの大きさで①鋭角(a<90°)②90°③鈍角(a>90°)で場合分け
- 円周角の定理を用いて、直角三角形を作り、sinAとの関係を求める
正弦定理「a/sinA=b/sinB=c/sinC=2R」のうち「a/sinA=2R」の部分が証明できれば、b/sinB、c/sinCの部分も同様なので、今回はa/sinA=2Rの証明を行います。
図を使った証明なので、解説動画での解説がおすすめです。
(1)A<90°のとき
点Aを点Oを通る場所点A'へ移動させると
辺A'Bは円の中心を通る直線なので「直径」となります。
円の直径を通る三角形の円周角は90°なので、角Cは90°となります。
円周角の定義より、A=A'なので
sinA=sinA'
sinA=a/2R
となるので、
a/sinA=2Rが成り立つ。
(2)A=90°のとき
sin90°=1なので
a/sinA=2RのsinAに1を代入すると
a/1=2R
となり、aと2Rは同じBCを表しているので、成立します。
(3)A>90°のとき
円に内接する四角形の内角の和は180°なので
∠A'=180°−A
sinA=sin(180°-A')=sinA'
という関係が成り立ちます。
三角形A'BCは鋭角な三角形になるので、あとは(1)と同様に証明することができます。
図形への書き込みを見ながら解説を見たい方は、解説動画を確認してみてくださいね。
StanyOnline
StanyOnlineでは
- 最短経路の合格をサポートする「受験コーチング」
- 家庭学習で行き詰まった問題をチャットで解決できる「質問し放題チャット家庭教師」
- 東大、京大、早慶などの難関大講師が授業を行う「オンライン家庭教師」
などの、様々なオンラインサービスを提供しております。
「受験コーチング」、「質問し放題のチャット家庭教師」は1週間の無料体験、
「Zoomオンライン家庭教師」は1コマ(2000円分)を無料で体験いただけます。
ぜひお気軽にお問い合わせください!
\まずは無料で体験/











