チェバの定理の証明について解説します。
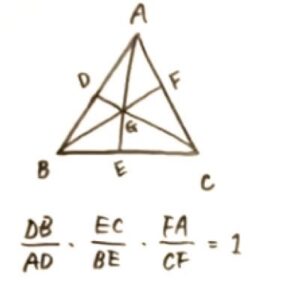
チェバの定理の証明を解説
今回の問題は、次の考え方で解きます。
面積比を用いて証明をする

まずは、上の三角形から次の三角形を抜き出します。
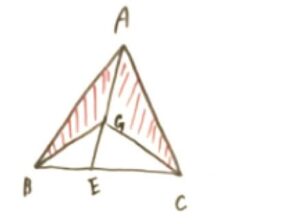
直線AEを延長して、点Bと点Cから垂線を引きます。
(点Bからの垂線とAEが交わる点をH、点Cからの垂線とAEが交わる点をIとする)
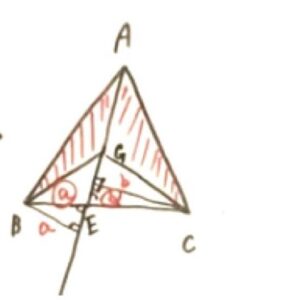
そのときにできる△BEHと△CEIは相似の関係となります。
△BEHと△CEIの相似の比をa:bとすると、AGBの面積:AGCの面積=a:b
当然BE:ECの比もa:bとなるので
AGBの面積:AGCの面積=BE:EC
のように、面積の比を辺の比で表すことができるのです。
この考えを使って、下図の青・赤・黒の三角形の面積の比を辺で表し、チェバの定理を証明します。
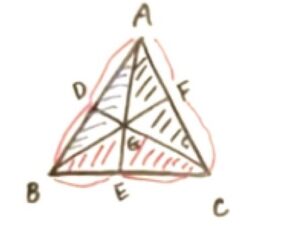
赤の三角形(△BGC)と青の三角形(△AGB)の比は、次のように表せる。
△BGC:△AGB=CF:FA
→△AGB/△BGC=FA/CF …①
黒の三角形(△AGC)と赤の三角形(△BGC)の比は、次のように表せる。
△AGC:△BGC=AD:DB
→△BGC/△AGC=DB/AD …②
青の三角形(△AGB)と黒の三角形(△AGC)の比は、次のように表せる。
△AGB:△AGC=BE:EC
→△AGC/△AGB=EC/BE …③
①②③をかけるとそれぞれが打ち消し合い、1になります。
DB/AD ✕ EC/BE ✕ FA/CF=△BGC/△AGC ✕ △AGC/△AGB ✕ △AGB/△BGC =1
StanyOnline
StanyOnlineでは
- 最短経路の合格をサポートする「受験コーチング」
- 家庭学習で行き詰まった問題をチャットで解決できる「質問し放題チャット家庭教師」
- 東大、京大、早慶などの難関大講師が授業を行う「オンライン家庭教師」
などの、様々なオンラインサービスを提供しております。
「受験コーチング」、「質問し放題のチャット家庭教師」は1週間の無料体験、
「Zoomオンライン家庭教師」は1コマ(2000円分)を無料で体験いただけます。
ぜひお気軽にお問い合わせください!
\まずは無料で体験/











