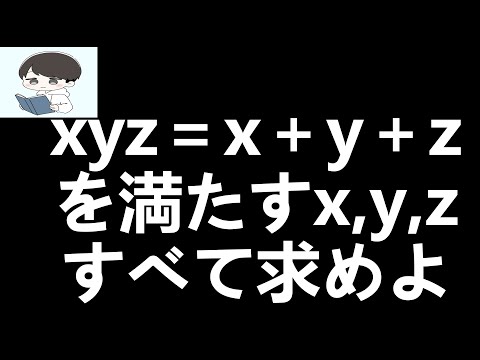今回は、二次関数が切り取る線分の長さを求める問題を解説します。
問題
放物線y=x2-ax+a-1がx軸から切り取る線分の長さが6である時、定数aの値を求めよ
一見難しそうに見える問題ですが、イメージができればすぐに解ける問題なので、理解できるようになりましょう。
動画でも解説をしています。詳しい解説を見たい方は下の動画をご覧ください。
二次関数が切り取る線分の長さ問題|解き方のポイント
この問題を解くためには、x軸と放物線の図を書いて問題をイメージする必要があります。
まずは、y=x2-ax+a-1とx軸が交わる図を書いてみましょう。
(図の書き方がわからない方は、解説動画1:00〜を確認しましょう)
x軸と放物線の交点を左からαとβとすると、求める長さはβ-αとなります。
x軸との交点なので、x2-ax+a-1を因数分解していきましょう。
因数分解
x2-ax+a-1=0
(x-1)(x+1-a)=0
X=1,a-1
今回はaの値がわからないので、aを場合分けして考えます。
場合分け1
1)a≧2のとき
a-1≧1
a-1-1=a-2=6
a=8
場合分け2
ii)a<2のとき
1>a-1
1-(a-1)=2-a=6
a=-4
どちらも場合分けの条件を満たしているので、a=-4,8となります。
答え -4,8
補足
一般的な2次方程式とx軸からなる線分の長さは「解の公式」を使って、求めることもできます
その方法を知りたい方は、解説動画2:58〜で解説しているので、確認してみてくださいね。
StanyOnline
StanyOnlineでは
- 最短経路の合格をサポートする「受験コーチング」
- 家庭学習で行き詰まった問題をチャットで解決できる「質問し放題チャット家庭教師」
- 東大、京大、早慶などの難関大講師が授業を行う「オンライン家庭教師」
などの、様々なオンラインサービスを提供しております。
「受験コーチング」、「質問し放題のチャット家庭教師」は1週間の無料体験、
「Zoomオンライン家庭教師」は1コマ(2000円分)を無料で体験いただけます。
ぜひお気軽にお問い合わせください!
\まずは無料で体験/