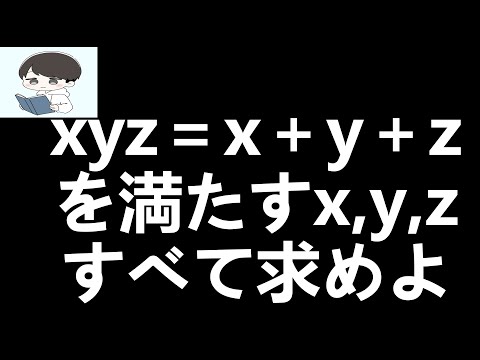今回は、整数問題(倍数を使う問題の解き方)を解説します。
問題
nは自然数とする。n+3は6の倍数であり、n+1は8の倍数であるとき、n+9は24の倍数であることを証明せよ。
動画の解説もあります。
3分でわかりやすく解説したので、確認してみてくださいね▼
【整数問題】倍数を使う問題の解き方を解説
今回の問題は、次の考え方で解きます。
考え方
n+3=6k、n+1=8L(エル)と置いて、n+9をkとLを用いて表す
※l(エル)はPC表記では1(イチ)と混同するので、今回は大文字表記のLを用います。
まずは
n+3=6k …①
n+1=8L …②
と置き、①②を用いて「n+9」を表します。
①を使って表す
n+9=(n+3)+6=6k+6=6(k+1)
②を使って表す
n+9=(n+1)+8=8L+8=8(L+1)
つまり
6(k+1)=8(L+1)
両辺2で割ると
3(k+1)=4(L+1)
3と4は互いに素(共通の約数が1だけ)なので、k+1は4の倍数。
k+1=4t …③ と置き
③を6(k+1)に代入すると
6(k+1)=6 ✕ 4t=24t (tは自然数)
6(k+1)=n+9なので
n+9=24t
よって、n+9は24の倍数である。
解き方がイメージしにくかった人は、一度解説動画で確認してみてくださいね。
StanyOnline
StanyOnlineでは
- 最短経路の合格をサポートする「受験コーチング」
- 家庭学習で行き詰まった問題をチャットで解決できる「質問し放題チャット家庭教師」
- 東大、京大、早慶などの難関大講師が授業を行う「オンライン家庭教師」
などの、様々なオンラインサービスを提供しております。
「受験コーチング」、「質問し放題のチャット家庭教師」は1週間の無料体験、
「Zoomオンライン家庭教師」は1コマ(2000円分)を無料で体験いただけます。
ぜひお気軽にお問い合わせください!
\まずは無料で体験/