今回は、受験生が苦手とする「軌跡」の問題を解説します。
問題
2点A(6,0)、B(3,3)と円x2+y2=9 上を動く点Qを3つの頂点とする。
三角形の重心Gの軌跡を求めよ。
図に表すと以下のようになります。
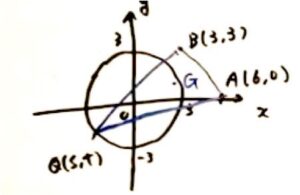
図形を用いた問題なので、動画での解説がおすすめです▼
【図形と方程式】三角形の重心の軌跡を求める方法

今回の問題は、次の考え方で解きます。
考え方
求める重心Gの軌跡を(x,y)、点Qを(s,t)と置いて、x,yの式を導く
求める重心Gの軌跡を(x,y)、点Qを(s,t)と置くと
Qは、x2+y2=9 上を動くので
s2+t2=9 …① が成り立つ。
Q(s,t)と定点(点Aと点B)を使って、Gを表していきます。
x=6+3+s/3
(↑点Aの6と、点Bの3と、点Qのsを足して3で割る)
上の式を変形すると
S=3x-9 …②
y=0+3+t/3
(↑点Aの0と、点Bの3と、点Qのtを足して3で割る)
上の式を変形すると
t=3y-3 …③
②と③を①に代入すると
(3x-9)2+(3y-3)2=9
両辺9で割ると
(x-3)2+(y-1)2=1
この式がどういう軌跡を描いているかを記述すればよい。
答え 中心(3,1)、半径1の円
問題がイメージしにくかった人は、一度解説動画で確認してみてくださいね。
StanyOnline
StanyOnlineでは
- 最短経路の合格をサポートする「受験コーチング」
- 家庭学習で行き詰まった問題をチャットで解決できる「質問し放題チャット家庭教師」
- 東大、京大、早慶などの難関大講師が授業を行う「オンライン家庭教師」
などの、様々なオンラインサービスを提供しております。
「受験コーチング」、「質問し放題のチャット家庭教師」は1週間の無料体験、
「Zoomオンライン家庭教師」は1コマ(2000円分)を無料で体験いただけます。
ぜひお気軽にお問い合わせください!
\まずは無料で体験/











